# Robot Baseball: Jane Street October 2025 monthly puzzle
Table of Contents
After a recent breakup, I needed something to distract myself and decided to work on Jane Street’s puzzle of the month.
If you’re just interested in the solution script, it is available here
Problem Analysis
The puzzle reads
The Artificial Automaton Athletics Association (Quad-A) is at it again, to compete with postseason baseball they are developing a Robot Baseball competition. Games are composed of a series of independent at-bats in which the batter is trying to maximize expected score and the pitcher is trying to minimize expected score.
An at-bat is a series of pitches with a running count of balls and strikes, both starting at zero. For each pitch, the pitcher decides whether to throw a ball or strike, and the batter decides whether to wait or swing; these decisions are made secretly and simultaneously. The results of these choices are as follows.
- If the pitcher throws a ball and the batter waits, the count of balls is incremented by 1.
- If the pitcher throws a strike and the batter waits, the count of strikes is incremented by 1.
- If the pitcher throws a ball and the batter swings, the count of strikes is incremented by 1.
- If the pitcher throws a strike and the batter swings, with probability p the batter hits a home run1 and with probability 1-p the count of strikes is incremented by 1.
An at-bat ends when either:
- The count of balls reaches 4, in which case the batter receives 1 point.
- The count of strikes reaches 3, in which case the batter receives 0 points.
- The batter hits a home run, in which case the batter receives 4 points.
By varying the size of the strike zone, Quad-A can adjust the value p, the probability a pitched strike that is swung at results in a home run. They have found that viewers are most excited by at-bats that reach a full count, that is, the at-bats that reach the state of three balls and two strikes. Let q be the probability of at-bats reaching full count; q is dependent on p. Assume the batter and pitcher are both using optimal mixed strategies and Quad-A has chosen the p that maximizes q. Find this q, the maximal probability at-bats reach full count, to ten decimal places.
This is quite clearly some sort of game theory problem, in which one party seeks to minimize a particular value (num of points) and the other seeks to maximise the same value.
The problem is really wordy and is probably best displayed in some sort of table
| Pitcher/Batter | Ball | Strike |
|---|---|---|
| Swing | +1 Strike | p: homerun / p’: +1 Strike |
| Wait | +1 Ball | +1 Strike |
Now the question we first have to ask ourselves is: is there a dominant strategy? Say p=0. Then, the pitcher would always strike as this always leads to +1 Strike, and the batter would always wait. Therefore, we would always end up in a +1 Strike and the game would end in 3 rounds with 0 points.
However, since the problem seems to imply the existence of a mixed strategy when p is set in such a way that maximises the probability of a full count, lets assume that there is no dominant strategy.
Furthermore, the optimal strategy probably depends on the state of the game. Therefore, let us begin by modelling this state of the game.
Thought process
Call the state of the game S(b,s), where b is the number of current balls and s is the number of current strikes.
Then call the expected value of each state E(S,p,x,y), where S is the state of the game, p is the probability of a homerun when we have a Strike/Swing scenario, and x and y are the probabilities of the pitcher choosing a ball and the batter choosing to wait. Alternatively, you could notate E(b,s,p,x,y) for simplicity.
The goal of the pitcher is to minimise the value of the state and the goal of the batter is to maximise it.
Now, we use some logic to “simplify” the problem.
Given some state S, lets say that for the pitcher, and , where E is the expected points of a specific action.
In this scenario, one can clearly tell that the pitcher should always Ball, as this minimizes the expected points. Therefore, the pitcher should always choose to throw a Ball here.
It is often confusing to those new to game theory on why players must be indifferent between actions in a mixed, optimal strategy, but allow me to present a intuitive argument for this.
Keep in mind that a nash equilibrium strategy assumes that both players have full knowledge of the other person’s strategy.
Consider the following scenario:
- If the batter chooses his probability of waiting in such a way that throwing a ball is always better for the pitcher, then the pitcher will always choose a ball.
- Therefore, since the batter always chooses a wait since that will mean that he will always get 1 point.
- However, if the batter always chooses to wait, the pitcher is now not incentivised to choose a ball, and will therefore be more inclined to choose to strike.
- Therefore, the pitcher will increase his probability of striking. In return, the batter will choose to wait more, and this “process” will happen until they eventually reach a state where the batter and striker have no preference between either action.
Therefore, at the equilibrium, the “payoff” or inversely, the “cost” of each action for a player must be the same.
This insight thus allows us to mathematically represent the optimal strategies
The value of the state E(x,y,b,s) can thus be calculated as follows
Remember that x = probability of ball, y = probability of wait, b = num of balls, s = num of strikes
Pitcher’s equilibrium
The expected value of the pitcher choosing to throw a ball is as follows (forgive the notation)
The expected value of the pitcher choosing to throw a strike is as follows
Additionally, we know that these two values must be equal for indifference. Therefore,
Batter’s equilibrium
Likewise, the expected value of the batter choosing to wait is as follows
The expected value of the batter swinging is as follows
And therefore,
Solution walkthrough
What a coincidence! It seems that the equations for both the batter’s and the pitcher’s optimal strategies are the same!
Furtheremore, we know that there are some terminal states of the value of a state!
Eg. and for any and
We can then now proceed to implement this in code with some recursion
First, write the function V(b,s,p) that calculates the value of a state given b,s,p
# returns the value function for state S(b,s)V_cache = {} # used a cache here to speed up the calculation -> we're using vanilla python w/o the aid of numpy etc which is pretty slow so this is necessarydef V(b,s,p): if b == 4: # terminal state for 4 balls return 1 if s == 3: # terminal state for 3 strikes return 0 key = (b, s) # cache lookup for speed if key in V_cache: return V_cache[key] else: x_val = x(b, s, p) # we will write these functions later on y_val = y(b, s, p) result = ( x_val * y_val * V(b+1,s,p) + x_val * (1 - y_val) * V(b,s+1,p) + (1 - x_val) * y_val * V(b,s+1,p) + 4 * p * (1 - x_val) * (1 - y_val) + (1 - x_val) * (1 - y_val) * (1 - p) * V(b,s+1,p) ) V_cache[key] = result return resultNext, write functions x and y, which calculate the optimal strategies given the value functions of the next states
# returns the optimal frequency for throwing a balldef x(b,s,p): return (p * (4 - V(b,s+1,p))) / (V(b+1,s,p) - V(b,s+1,p) + p * (4 - V(b,s+1,p)))
# returns the optimal frequency for waitingdef y(b,s,p): return (p * (4 - V(b,s+1,p))) / (V(b+1,s,p) - V(b,s+1,p) + p * (4 - V(b,s+1,p)))Lastly, since we want to find the value of p that maximises q, the probabilities that the at-bats reach full count, write a function q, that returns the probability of reaching state S(b,s)
The formula for Q is as follows
Q_cache = {} # again, cache here used for speed# returns the probability of reaching state S(b,s)def Q(b,s,p): # print((b,s,p)) if b == 0 and s == 0: # we always start at S(0,0), so we have a probability of 1 of reaching this state return 1
if b < 0 or s < 0: # we can never reach values with b < 0 or s < 0 return 0
key = (b,s) if key in Q_cache: return Q_cache[key]
else: res = ( x(b-1,s,p) * y(b-1,s,p) * Q(b-1,s,p) + x(b,s-1,p) * (1 - y(b,s-1,p)) * Q(b,s-1,p) + (1 - x(b,s-1,p)) * y(b,s-1,p) * Q(b,s-1,p) + (1 - x(b,s-1,p)) * (1 - y(b,s-1,p)) * (1 - p) * Q(b,s-1,p) )
Q_cache[key] = res return resNow, all we need to do is find this p that minimizes q.
Lets plot a graph of q as p progresses.
import matplotlib.pyplot as pltx_vals = []y_vals = []for i in range(1,101): V_cache = {} Q_cache = {} x_vals.append(i/100) y_vals.append(Q(3,2,i/100))
plt.xlabel("p value")plt.ylabel("Q(3,2,p)")plt.plot(x_vals, y_vals)plt.show()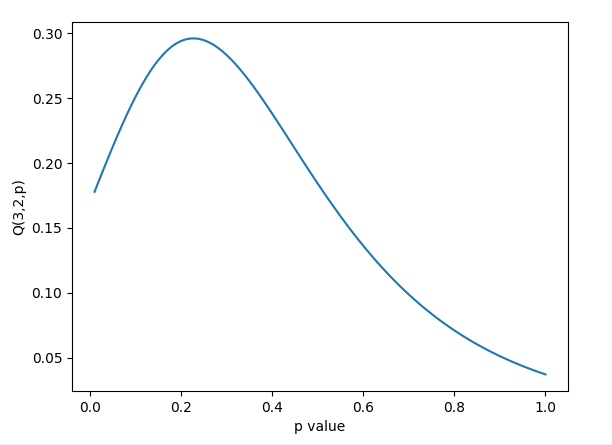
As you can see, the value of Q peaks somewhere around
We could then bruteforce all values to 10dp between 0.2-0.25(one of my friends wrote this script in c++ and did this)
However, it would probably be faster and more bearable to use some sort of optimised search function given that our code is not terribly fast, and 10dp isn’t that hard to narrow down.
Thankfully, scipy has a pretty good minimize_scalar function. Since we want to maximise Q instead of minimizing it, we could just aim to minimize -Q or (1-Q)
from scipy.optimize import minimize_scalardef compute_q(p): V_cache.clear() Q_cache.clear() return -Q(3,2,p)res = minimize_scalar( lambda p: compute_q(p), bounds=(0,1), method='bounded', options= { 'disp': True })
print("Optimal p:", f"{res.x:.10f}", "Resultant Q = ", f"{Q(3,2,res.x):.10f}") # 0.2269743428955392Optimal p: 0.2269743429 Resultant Q = 0.2959679933
And that’s the puzzle solved! 😆